TNPSC General Scientific Laws -இயக்கவியலில் பொது அறிவியல் விதிகள்

 

TNPSC General Scientific Laws

பாஸ்கல் விதி

• பிரஞ்சு அறிவியல் அறிஞர் பிளெய்ஸ் பாஸ்கல் என்பவர் ஓய்வில் உள்ள ஒரு பாய்மத்தில் சம உயரத்தில் உள்ள அனைத்து புள்ளிகளிலும் அழுத்தம் சமமாக உள்ளது என கண்டறிந்தார். பாஸ்கல் விதியின் படி ஒரு ‘’திரவத்தில் உள்ள ஒரு புள்ளியில் அழுத்தம் மாறினால் அந்த மாறுபாடு மதிப்பு குறையாமல் திரவம் முழுவதற்கும் பரப்பப்படுகிறது’’

1. நீர்மங்களின் அடிப்பகுதியில் அழுத்தம், அந்நீர்மத்தின் மொத்த உயரத்தைப் பொருத்தது.
2. நீர்மங்கள் அவை உள்ள கலனின் பக்கங்களிலும் அழுத்தத்தை கொடுக்கின்றன.
3. திரவங்கள் ஒரே ஆழத்தில், ஒரே அளவு அழுத்தத்தைக் கொடுக்கின்றன.
4. திரவங்களில் ஆழம் அதிகரிக்க அழுத்தம் அதிகரிக்கும்.
5. திரவங்களின் அழுத்தம் அவற்றின் அடர்த்தியைப் பொருத்தது.

எதிரொளிப்பு விதி

1. சமதள ஆடிகள் ஏற்படுத்தும் விளைவை அனைத்துப் பொருள்களும் ஏற்படுத்தமுடியாது. ஓர் ஒளிக்கதிரானது பளபளப்பான, மென்மையான ஒளிரும் பரப்பின்மீது படும்போது, அது திருப்பி அனுப்பப்படுகிறது. இவ்வாறு ஒளியானது பளபளப்பான, மென்மையான, ஒளிரும் பரப்பில் பட்டு திரும்பும் நிகழ்வே ஒளி எதிரொளித்தல் என்று அழைக்கப்படுகிறது.
2. ஒளி எதிரொளித்தலில் இரு கதிர்கள் ஈடுபடுகின்றன. அவை: படுகதிர் மற்றும் எதிரொளிப்புக் கதிர் ஒரு ஊடகத்திலுள்ள பளபளப்பான எதிரொளிக்கும் தளத்தின் மீது விழக்கூடிய ஒளிக்கதிர் படுகதிர் எனப்படும். ஒளியானது அப்பரப்பின்மீது பட்டபிறகு, அதே ஊடகத்திற்கே திரும்ப வருகிறது. இந்த ஒளிக்கதிர் 'எதிரொளிப்புக் கதிர்' எனப்படும். எதிரொளிக்கும் பரப்பில், ஒளிக்கதிர் படும் புள்ளியில் கற்பனையாக வரையப்பட்ட செங்குத்துக் கோடு 'குத்துக்கோடு' எனப்படும்.

படுகதிர், எதிரொளிப்புக்கதிர் மற்றும் குத்துக்கோடு ஆகியவற்றிற்கு இடையே உள்ள தொடர்பு எதிரொளிப்பு விதிகளாக கொடுக்கப்பட்டுள்ளன. அவை பின்வருமாறு:

1. படுகதிர், எதிரொளிப்புக் கதிர் மற்றும் படுபுள்ளியில் வரையப்பட்ட குத்துக்கோடு ஆகிய அனைத்தும் ஒரே தளத்தில் அமைந்துள்ளன.

2. படுகோணமும் (i), எதிரொளிப்புக் கோணமும் (r) எப்போதும் சமமாகவே இருக்கும்.

வெள்ளியே மிகச்சிறந்த ஒளி எதிரொளிப்புப் பொருளாகும். எனவேதான், ஆடிகளை உருவாக்குவதற்கு கண்ணாடித்துண்டின் பரப்பின்மீது மெல்லிய படலமாக வெள்ளி பூசப்படுகிறது

ஆற்றல் அழிவின்மை விதி

• ஆற்றலை, ஆக்கவோ, அழிக்கவோ முடியாது.
• ஒருவகை ஆற்றலை மற்றொரு வகை ஆற்றலாக மாற்ற முடியும்.
• எந்த ஓர் ஆற்றல் மாற்றத்திலும் மொத்த ஆற்றலின் அளவு மாறாமல் இருக்கும்.

ஆர்க்கிமிடிஸ் தத்துவம்

1. பாஸ்கல் விதியின் விளைவே ஆர்க்கிமிடிஸின் தத்துவமாகும். வரலாற்றுக் குறிப்புகளின் படி, குளியல் தொட்டியில் அமர்ந்திருக்கும் போது தனது எடையில் ஏற்பட்ட வெளிப்படையான இழப்பைக் கவனித்தபிறகு 'நீர்நிலை சமநிலையின் (hydrostatic balance) தத்துவத்தை ஆர்க்கிமிடிஸ் உருவாக்கினார். அவர் இந்தத் தத்துவத்தைக் கண்டுபிடித்தவுடன் ‘யுரேகா’ என்று அலறிக்கொண்டே குளியல் தொட்டியிலிருந்து வெளியே ஓடினார் என்று கூறப்படுகிறது. ஒரு பொருளானது பாய்மங்களில் மூழ்கும் போது, அப்பொருள் இடப்பெயர்ச்சி செய்த பாய்மத்தின் எடைக்குச் சமமான செங்குத்தான மிதப்புவிசையை அது உணரும்" என்று ஆர்க்கிமிடிஸ் தத்துவம் கூறுகிறது.
2. ஒருபொருள் முழுமையாகவோ பகுதியாகவோ ஓய்வுநிலையில் உள்ள பாய்மத்தில் மூழ்கும் போது, அப்பொருள் இடப்பெயர்ச்சி செய்த பாய்மத்தின் எடைக்குச் சமமான மேல்நோக்கு விசையை உணரும். இந்த மேல்நோக்கு விசையினால் பொருள் தன் எடையின் ஒரு பகுதியை இழக்கிறது. எடையில் ஏற்பட்ட இந்த இழப்பு மேல்நோக்கு விசைக்குச் சமமாக உள்ளது.
3. எனவே, பொருளொன்று முழுமையாகவோ அல்லது பகுதியாகவோ பாய்மங்களில் மூழ்கும் போது, 

மேல் நோக்கு விசை = இடப்பெ யர்ச்சி செய்யப்பட்ட  பாய்மத்தின் எடை              = பொருளின் தோற்ற எடை இழப்பு

பொருளின் தோற்ற எடை இழப்பு  = காற்றில் பொ ருளின் எடை –  மேல் நோக்கு விசை  (இடப்பெ யர்ச்சி செய்யப்பட்ட நீரின் எடை)

ஒரு பொருள், பாய்மத்தில் (திரவம் (அ) வாயு) தங்கு தடையின்றி முழ்கியிருக்கும் போது, அது இழப்பதாகத் தோன்றும் எடை, வெளியேற்றப்படும் பாய்மத்தின் எடைக்குச் சமமாக இருக்கும்.

மிதத்தல் விதி (Law of Floatation) 

1. படகுகள், கப்பல்கள் மற்றும் சில மரப்பொருள்கள் நீரின் மேற்பகுதியில் இயங்குவது நன்கு அறிந்த ஒன்றாகும். அவை மிதக்கிறது எனலாம். பாய்மத்தின் மேல் மட்டங்களுக்கு உயர்கின்ற அல்லது பாய்மத்தின் மேற்பரப்பில் நிலைத்து நிற்கும் ஒரு பொருளின் தன்மை மிதத்தல் என வரையறுக்கப்படுகிறது. 
2. ‘’பொருளின் மூழ்கிய பகுதி இடம்பெயரச்செய்த திரவத்தின் எடை, பொருளின் எடைக்கு சமமானால் அந்தப் பொருள் அத்திரவத்தில் மிதக்கும்’’ என்பது மிதத்தல் விதியாகும். உதாரணமாக, 300 kg எடையுள்ள (ஏறத்தாழ 3000 N) ஒரு மரத்தாலான பொருள் நீரில் மிதக்கும்போது 300 kg (ஏறத்தாழ 3000 N) நீரை இடம்பெயரச் செய்கிறது.

• குறிப்பு : ஒரு பொருள் மிதந்தால் குறிப்பு இடம்பெயர்ந்த பாய்மத்தின் பருமன் மூழ்கிய பொருளின் பருமனுக்கு சமமாக உள்ளது, மற்றும் மூழ்கிய பொருளின் பருமனின் சதவீதம் பொருளின் அது மிதக்கும் பாய்மத்தின் அடர்தியைப் பொருத்த ஒப்படர்த்திக்கு சமமாகும். உதாரணமாக 0.9 gcm-3 அடர்த்தி கொண்ட ஒரு பனிக்கட்டி 1.0 gcm-3 அடர்த்தி கொண்ட தூய நீரில் மிதந்தால், நீரில் மூழ்கிய பொருளின் பருமனின் சதவீதமானது 0.9 gcm-3 / 1.0 gcm-3 × 100% = 90%.  மாறாக, அதே பனிக்கட்டி 1.3 gcm-3, அடர்த்தி கொண்ட கடல் நீரில் மிதந்தால், கடல் நீரில் மூழ்கிய பொருளின் பருமனின் சதவீதமானது 0.9 gcm-3 / 1.0 gcm-3 × 100% = 69.23% மட்டுமே.

 பாயில் விதி, சார்லஸ் விதி மற்றும் நல்லியல்பு வாயு விதி:  

1. பருமன் V கொண்ட கொள்கலனில் குறைந்த அழுத்தத்தில் (அடர்த்தி) உள்ள வாயு ஒன்றினைக் கொண்டு நிகழ்த்தப்பட்ட சோதனையிலிருந்து பின்வரும் முடிவுகள் கிடைக்கின்றன.
2. மாறா வெப்பநிலையிலுள்ள வாயு ஒன்றின் அழுத்தம், அதன் பருமனுக்கு எதிர்விகிதத்திலிருக்கும் P ∝ 1/V. இதனை இராபர்ட் பாயில் (Robert Boyle) என்பவர் (1627-1691) கண்டறிந்தார். எனவே இவ்விதி பாயில்விதி என அழைக்கப்படுகிறது.
3. மாறா அழுத்தத்திலிருந்து வாயு ஒன்றின்பருமன், அதன் வெப்பநிலைக்கு (கெல்வின்) நேர்த்தகவிலிருக்கும். V ∝ T இதனை ஜாக்ஸ் சார்லஸ் (Jacques Charles) (1743-1823) என்பவர் கண்டறிந்தார். எனவே இவ்விதி சார்லஸ்விதி என்று அழைக்கப்படுகிறது. 
4. இவ்விரண்டு விதிகளையும் ஒன்றிணைக்கும்போது பின்வரும் சமன்பாடு கிடைக்கும். PV = CT இங்கு C என்பது நேர்க்குறி கொண்ட மாறிலியாகும். இந்த நேர்க்குறி மாறிலி C கொள்கலனிலுள்ள துகள்களின் எண்ணிக்கைக்கு நேர்விகிதத்தில் இருக்கும் என்பதை பின்வரும் விவாதத்தின் மூலம் அறியலாம். ஒத்த பருமன் V, அழுத்தம் P மற்றும் வெப்பநிலை T, கொண்ட ஒரே வகையான வாயுவால் இவ்விரண்டு கொள்கலன்களும் நிரப்பப்பட்டுள்ளன என்க. இரண்டு கொள்கலனிலும் உள்ள வாயு மேலே குறிப்பிட்டுள்ள PV = CT என்ற சமன்பாட்டின்படி செயல்படும். இவ்விரண்டு தனித்தனியான கொள்கலனையும் படம் 8.2 இல் காட்டியுள்ளவாறு ஒரே அமைப்பாகக் கருதினால் அவ்வாயுவின் அழுத்தம் மற்றும் வெப்பநிலை ஒரே மதிப்பினைப் பெறும் ஆனால் பருமனும் மற்றும் வெப்பநிலை துகள்களின் எண்ணிக்கையும் இரண்டு மடங்காகும்
5. ஆகவே வாயுவின் பருமன் 2V மற்றும் துகள்களின் எண்ணிக்கை 2C. எனவே நல்லியல்பு வாயுச் சமன்பாடு P(2V) / T = 2C. இச்சமன்பாடு நமக்கு உணர்த்துவது என்னவென்றால் நேர்க்குறி மாறிலி C கண்டிப்பாக வாயுவிலுள்ள துகள்களின் எண்ணிக்கையை சார்ந்திருக்கும் என்பதாகும்.
6. மேலும் இதன் பரிமாணம் [PV/T] = JK-1 இந்த நேர்க்குறி மாறிலி C ஐ துகள்களின் எண்ணிக்கை (N) யின் k மடங்கு என எழுதலாம். இங்கு k என்பது பொது மாறிலியான போல்ட்ஸ்மென் மாறிலியாகும். (1.381×10−23 JK−1)  

டாப்ளர் விளைவு

1. ஒலி மூலத்திற்கும் அவ்வொலியைக் கேட்பவருக்கும் இடையே உள்ள சார்பு இயக்கத்தினால் இவ்விளைவு ஏற்படுகிறது. இயக்கத்தினால் ஏற்படும் இத்தகைய அதிர்வெண் மாற்றத்தை ஆஸ்திரிய நாட்டைச் சேர்ந்த கணிதவியலாளரும் இயற்பியலாளருமான யோகாண் கிறிஸ்டியன் டாப்ளர் (1803-1853) என்பவர் முதலில் ஆராய்ந்தார்.
2. ஒலிமூலத்திற்கும் கேட்பவருக்கும் இடையே ஒரு சார்பு இயக்கம் உள்ளபோது ஒலி மூலத்தில் இருந்து வரும் ஒலியின் அதிர்வெண்ணும் அதைக் கேட்பவரால் உணரப்படும் ஒலியின் அதிர்வெண்ணும் மாறுபட்டு இருக்கும். இதுவே டாப்ளர் விளைவு எனப்படும்

நியூட்டன் முதல் விதி / இயக்கத்திற்கான முதல் விதி

• சமமற்ற புறவிசையொன்று செயல்பட்டு மாற்றும் வரை எந்த ஒரு பொருளும் தனது ஓய்வு நிலையையோ அல்லது நேர்க்கோட்டில் அமைந்த சீரான இயக்க நிலையையோ மாற்றிக் கொள்ளாமல் தொடர்ந்து அதே நிலையில் இருக்கும்.

குறிப்பு : 

• ஒலியின் வேகத்தில் ஏற்படும் மாறுபாடு (ஒலி மூலம் ஓய்விலும் கேட்பவர் நகரும் போது )அல்லது ஒலியின் அலைநீளத்தில் ஏற்படும் மாறுபாடு (கேட்பவர் ஓய்விலும் ஒலி மூலம் நகரும் போது) காரணமாகவே அதிர்வெண் மாறுபாடு ஏற்படுகிறது என்பதை கவனிப்பது முக்கியமாகும்.
• ஒலி மூலம் மற்றும் கேட்பவர் என இரண்டும் நகரும் போது, ஒலியின் வேக மாறுபாடு மற்றும் ஒலியின் அலைநீள மாறுபாடுஆகிய இரண்டின் காரணமாக அதிர்வெண் மாறுபாடு ஏற்படுகிறது.
• ஒலி மூலத்தின் முன்புறம் உள்ள நிலையான கேட்பவரால் ஒலியை கேட்க முடியாது. ஒலி அலைகளானது மூலத்திற்கு பின்புறம் அமைவதே காரணமாகும். 
• இத்தகைய வேகங்களில், புதிதாக உருவாகும் அலைகளும் முன் கணத்தில் உருவான அலைகளும் ஆக்கக் குறுக்கீட்டு விளைவினால் மிகப்பெரிய வீச்சுடன் கூடிய ஒலியை உருவாக்கின்றன. இதை 'ஒலி முழக்கம்' (sonic boom) அல்லது 'அதிர்ச்சி அலை' (shock wave) என்கிறோம்.

நியூட்டனின் இரண்டாம் இயக்க விதி

• பொருளின் மாறுபாட்டு வீதம், அதன் மீது செயல்படும் விசைக்கு நேர்த்தகவில் அமைவதோடு அவ்விசையின் திசையிலேயே அமையும்.
• F=ma
• F - விசை ; m - நிறை ; a - முடுக்கம்

நியூட்டனின் மூன்றாம் இயக்க விதி

• ஒவ்வொரு வினைக்கும் அதற்குச் சமமான ஆனால் எதிர் திசையில் செயல்படும் ஓர் எதிர்வினை உண்டு.

நியூட்டனின் ஈர்ப்பு விதி

1. நியூட்டனின் ஈர்ப்பியல் விதிப்படி, இருப் பொருட்களுக்கிடையேயுள்ள ஈர்ப்பு விசையானது, அவற்றின் நிறைகளின் பெருக்கற்பலனுக்கு நேர்த்தகவிலும், அவற்றிற்கிடையேயுள்ள தொலைவின் இருமடிக்கு எதிர்த்தகவிலும் இருக்கும். அதாவது, m1 ,m2 என்பன முறையே இரு பொருள்களின் நிறைகள் எனவும் r என்பது அவற்றிற்கு இடைப்பட்ட தொலைவு எனவும் கொண்டால், இவ்விரு பொருள்களுக்கு இடையேயான ஈர்ப்பு விசை, 
2. G - மாறிலி ;
3. m1, m2 - நிறைகள் ; d- பொருள்களுக்கிடையேயான தொலைவு

ஓம் விதி

1. ஜார்ஜ் சைமன் ஓம் என்ற ஜெர்மன் இயற்பியலாளர் மின்னோட்டம் மற்றும் மின்னழுத்த வேறுபாடு ஆகியவற்றிற்கிடையேயான தொடர்பினை நிறுவினார். இதுவே ஓம் விதி எனப்படும்.
2. இவ்விதியின்படி மாறா வெப்பநிலையில், கடத்தி ஒன்றின் வழியே பாயும் சீரான மின்னோட்டம் கடத்தியின் முனைகளுக்கிடையே உள்ள மின்னழுத்த வேறுபாட்டிற்கு நேர்தகவில் அமையும்.
3. ஒரு [மின்கடத்தி]யில் மின்னழுத்ததைக் கொடுக்கும் போது, அதில் மின்னோட்டம் நடை பெறுகின்றது. அந்த மின்னோட்டத்தின் அளவு அதில் கொடுக்கப்படும் மின்னழுத்தத்தின் அளவைப் பொறுத்திருக்கும். எடுத்துக் காட்டாக, R என்ற மின்தடையம் கொண்ட ஒரு மின் கடத்தியின்(எ.கா. உலோகங்கள்,மாழைகள்) இரு முனைகளுக்கிடையே, V என்ற அளவு மின்னழுத்தம்(voltage) கொடுக்கும் போது, I என்ற அளவு மின்னோட்டம்(current) பாய்கிறது என்றால், அந்த மின்னோட்டத்தின் அளவைக் கீழ்க் கண்டவாறு கணக்கிடலாம்:

${\displaystyle �=\frac{�}{�}}$.

• V= IR
• R - மின்தடை
• V - மின்னழுத்தம்
• I - மின்னோட்டம்

ஜூல் வெப்ப விதி

1. ஒரு மின்தடையாக்கியின் வழியாக மின்னோட்டம் பாயும் போது, மின்தடையாக்கிக்கு அளிக்கப்படும் மின்னாற்றலில் சிறிதளவு வெப்ப ஆற்றலாக மாற்றப்பட்டு வீணாகிறது. மின்னோட்டத்தின் இந்த வெப்பவிளைவே ஜுல் வெப்ப விளைவு எனப்படும். மின்னோட்டம் எவ்வாறு வெப்ப ஆற்றலை ஏற்படுத்துகிறதோ அதேபோல் வெப்ப ஆற்றலை தகுந்த முறையில் பயன்படுத்தி மின்னியக்கு விசையை (மின் ஆற்றல்) பெற முடியும். இதுவே வெப்ப மின் விளைவு எனப்படும்.
2. ஒரு மின்தடையில் உருவாக்கப்படும் வெப்பமானது, குறிப்பிட்ட மின்தடைக்கு அதன் வழியே பாயும்.

ஜுலின் விதிப்படி, ஒரு மின்சுற்றில் மின்னோட்டம் பாய்வதால் உருவாக்கப்படும் வெப்பமானது

• (i) மின்னோட்டத்தின் இருமடிக்கு நேர்த்தகவிலும்
• (ii) மின்சுற்றின் மின்தடைக்கு நேர்த்தகவிலும்
• (iii) மின்னோட்டம் பாயும் நேரத்திற்குநேர்த்தகவிலும் அமையும் 
• H = I2Rt ஜூல்
• H - வெப்பநிலை
• I - மின்னோட்டம்
• R - மின்தடை
• t - நேரம் (விநாடி)

பிளமிங் இடக்கை விதி

இடக்கையின் கட்டைவிரல், சுட்டு விரல், நடுவிரல் ஆகிய மூன்றையும் ஒன்றுக்கொன்று செங்குத்தாக வைக்கவும்.

• சுட்டுவிரல் காந்தப் புலத்தின் திசையையும்
• நடுவிரல் மின்னோட்டத்தின் திசையையும் குறித்தால் கட்டைவிரல் கடத்தி இயங்கும் திசையை குறிக்கும்

பிளமிங் வலக்கை விதி

வலக்கையின் சுட்டுவிரல், நடுவிரல், பெருவிரல் மூன்றையும் ஒன்றுக்கொன்று நேர்க்குத்தாக வைக்கவும் .

• சுட்டுவிரல் காந்தப்புலத்தின் திசையையும்
• பெருவிரல் கடத்தி இயங்கும் திசையையும் குறித்தால்
• நடுவிரல் தூண்டு மின்னோட்டத்தின் திசையைக் குறிக்கும்.

ஒளிவிலகல் விதி

• படுகதிர், விலகுகதிர், படுபுள்ளியில் அவ்விரு ஊடகங்கள் சந்திக்கும் பரப்பிற்கு வரையப்பட்ட செங்குத்துக்கோடு ஆகியவை ஒரே தளத்தில் அமையும்.
• ஒளியானது ஓர் ஊடகத்திலிருந்து மற்றோர் ஊடகத்திற்கு செல்லும்.

ஸ்நெல் விதி

1. ஒளிக்கதிர் ஓர் ஊடகத்திலிருந்து, மற்றோர் ஊடகத்திற்குச் செல்லும்போது, படுகோணத்தின் சைன் மதிப்பிற்கும், விலகு கோணத்தின் சைன்மதிப்பிற்கும் இடையே உள்ள தகவானது அவ்விரு ஊடகங்களின் ஒளிவிலகல் எண்களின் தகவிற்கு சமம். இவ்விதி 'ஸ்நெல் விதி' என்றும் அழைக்கப்படுகிறது.
2. 
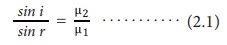
3. ஒளிவிலகல் எண்ணானது ஓர் ஊடகத்தில் ஒளிக்கதிரின் திசைவேகம் எவ்வாறு இருக்கும் என்பதைத் தெரிவிக்கின்றது. காற்றில் அல்லது வெற்றிடத்தில் ஒளியின் திசைவேகத்திற்கும் (c), மற்றோர் ஊடகத்தில் ஒளியின் திசைவேகத்திற்கும் (v) இடையே உள்ள தகவு ஒளிவிலகல் எண் (µ) என்றும் வரையறுக்கப்படுகிறது.
4. µ = c/v
5. ஒளியின் திசைவேகமானது ஒளிவிலகல் எண் அதிகம் உள்ள ஊடகத்தில் குறைவாகவும், ஒளிவிலகல் எண் குறைவாக உள்ள ஊடகத்தில் அதிகமாகவும் அமையும்.
6. ஓர் ஒளிக்கதிரானது அடர்வு மிகு ஊடகத்திலிருந்து அடர்வு குறைந்த ஊடகத்திற்குச் செல்லும்போது விலகு கதிர் செங்குத்து கோட்டை விட்டு விலகிச்செல்லும்
7. ஒளிக்கதிர் அடர்வு குறைந்த ஊடகத்திலிருந்து, அடர்வு மிகு ஊடகத்திற்குச் செல்லும் போது செங்குத்து கோட்டை நோக்கி விலகிச் செல்லும்.

வெக்டர்களின் முக்கோண விதி

• எண் மதிப்பிலும், திசையிலும் குறிக்கப்பட்ட இரு வெக்டர்கள் வரிசைப்படி ஒரு முக்கோணத்தில் அடுத்தடுத்தப் பக்கங்களாகக் கருதப்பட்டால், அவற்றின் தொகுப்பயன், எதிர்வரிசையில் அந்த முக்கோணத்தின் மூடிய பக்கமாக இருக்கும்.

நேர்க்கோட்டு உந்த அழிவின்மை விதி

1. அமைப்பு ஒன்றின் மொத்த உந்தம் எப்போதுமே மாறாது.
2. புறவிசைகளின் தாக்கம் கழி எனில், அமைப்பின் மொத்த உந்தம் மாறாமல் இருக்கும்

ஹீக் விதி

1. ஒரு கம்பியின் நீட்சிக்கும், அதில் ஏற்படும் மீள்விசைக்கும் இடையே உள்ள தொடர்பை விளக்கும்.
2. மீட்சி எல்லைக்குள் ஒரு பொருளின் திரிபானது அதை ஏற்படுத்தக் கூடிய தகைவுக்கு நேர்தகவில் உள்ளது.
3. தகைவு/திரிபு= மாறிலி 
4. இது மீட்சிக் குணம் எனப்படும்.

ஸ்டோக் விதி

1. அதிக பாகுநிலை கொண்ட நீர்மத்தினூடே கீழ்நோக்கி நகரும் ஒரு பொருள் அதனுடன் தொடர்பு கொண்ட ஏடுகளை இழுக்கும். இதனால் ஏடுகளுக்கிடையே ஒப்புமை இயக்கும் ஏற்படுகிறது.
2. இந்த ஒப்புமை இயக்கம் காரணமாக கீழ்நோக்கிய பொருளின் மீது பாகுநிலை (F) விசை செயல்படுகிறது. 

• i) கோளத்தின் ஆரம் (r) 
• ii) கோளத்தின் திசைவேகம் (v) மற்றும்
• iii) திரவத்தின் பாகியல் எண் η
• ஆகியவற்றைச் சார்ந்தது என்ற முடிவைப் பெற்றார். எனவே F ∝ ηx r yvz ⇒ F =kηxr y vz இங்கு k என்பது ஒரு பரிமாணமற்ற மாறிலி
• பரிமாணங்களைப் பயன்படுத்தி, மேற்கண்ட சமன்பாட்டை இவ்வாறு எழுதலாம்.
• [MLT – 2]  = k [ML−1T – 1] x ×[ L]y × [LT−1] z 
• தீர்வு காண, x = 1, y = 1 மற்றும் z = 1 எனவே F=kη rv
• சோதனைமூலம் k = 6π என ஸ்டோக் கண்டறிந்தார்.
• F= 6πη rv
• n – பாகியல் எண்
• a - கோள பொருளின் ஆரம்
• V - கோள வடிவ பொருளின் திசைவேகம்

ஆற்றல் சமபங்கீட்டு விதி

வெப்பம் சமநிலையில் இயங்கும் தொகுதியின் மொத்த ஆற்றல் தொகுதியின் அனைத்து உரிமைப்படிகளுக்கும் சமமாகப் பங்கிடப்படுகிறது.இது ஆற்றல் சம பங்கீட்டு விதியாகும்.

வெப்ப இயக்கவியலின் சுழி விதி

• தொகுதிகள் A, B, C யைக் கருத்தில் கொள்வோம்.
• இரு தொகுதிகள் (A, B) என்பன, தனித்தனியே மூன்றாவது தொகுதியுடன் (C) வெப்பச் சமநிலையில் இருந்தால், அம்மூன்று தொகுதிகளும் ஒன்றோடொன்று வெப்பச் சமநிலையில் இருக்கும்.

வெப்ப இயக்கவியலின் முதல் விதி

1. ஆற்றல் மாறாவிதியின் கூற்றே வெப்ப இயக்கவியலின் முதல் விதி ஆகும். நியூட்டனின் இயக்கவியலில் ஆற்றல் மாறாத்தன்மை பெரிய பொருள்களின் இயக்க ஆற்றல் மற்றும் நிலை ஆற்றலை உள்ளடக்கியுள்ளது. ஆனால் வெப்ப இயக்கவியலின் முதல் விதி வெப்பத்தையும் உள்ளடக்கியுள்ளது. இவ்விதியின்படி அமைப்பின் அக ஆற்றல் மாறுபாடானது (ΔU), அமைப்பிற்குக் கொடுக்கப்பட்ட வெப்பத்திற்கும் (Q) சூழலின் மீது அவ்வமைப்பு செய்த வேலைக்கும் (W) உள்ள வேறுபாட்டிற்குச் சமமாகும். கணிதமொழியில் இதனைப் பின்வருமாறு குறிப்பிடலாம்.
2. ஓர் அமைப்பிற்கு கொடுக்கப்ட்ட வெப்ப ஆற்றல், அமைப்பின் அக ஆற்றல் மாறுபாடு, மற்றும் அமைப்பினால் செய்யப்பட்ட வேலை, இவற்றின் கூடுதலுக்கு சமம்.

வெப்ப இயக்கவியலின் முதல் விதிக்கான சமன்பாடு இவ்வாறு கொடுக்கப்பட்டுள்ளது

ΔU = q + W

எங்கே,

• ΔU = அமைப்பின் உள் ஆற்றலில் மாற்றம்
• q = அமைப்பு மற்றும் சுற்றுப்புறங்களுக்கு இடையேயான வெப்ப பரிமாற்றத்தின் இயற்கணிதத் தொகை
• W = அதன் சுற்றுப்புறங்களுடனான அமைப்பின் வேலை தொடர்பு

வெப்ப இயக்கவியலின் இரண்டாம் விதி

இவ்விதி, ஆற்றல் மாறுபாட்டின் அளவு மற்றும் திசையைப் பற்றிக் கூறுகிறது.

கெல்வின் கூற்று

• ஒரு பொருளை, அதன் சூழலை விட, மிகக் குளிர்ந்த வெப்பநிலையைக் காட்டிலும், குறைவாக உள்ள வெப்பநிலைக்கு குளிர்விப்பதன் மூலம் அதனின்றும் தொடர்ந்து வேலையைப் பெற முடியாது.

கிளாசியஸின் கூற்று

• புற உதவியின்றி தானே இயங்கும் இயந்திரத்தின் மூலம் குறைந்த வெப்பநிலையில் உள்ள ஒரு பொருளிலிருந்து அதிக வெப்பநிலையிலுள்ள மற்றொரு பொருளுக்கு வெப்பத்தை மாற்ற இயலாது.

கெல்வின் பிளாங்க் கூற்று

• வெப்பத்தினை, வெப்ப மூலத்திலிருந்து பெற்று, அதற்குச் சமமான வேலையைச் செய்யும் ஒரு சுற்றில் இயங்கும் வெப்ப இயந்திரத்தினை அமைக்க இயலாது.

கிர்ச்சாஃப் விதி

• ஒரு குறிப்பிட்ட அலைநீளத்தின் மற்றும் வெப்பநிலையில் கதிர்வீச்சு திறனுக்கும் உட்கவர் திறனுக்கும் உள்ள தகவு மாறிலி.

வியனின் இடப்பெயர்ச்சி விதி

• வீனின் இடப்பெயர்ச்சி விதி (Wien's displacement law) கரும்பொருள் ஒன்றில் இருந்து எந்த வெப்பநிலையிலும் வெளியேறும் வெப்பக் கதிர்வீசலின் அதிக ஆற்றல் கொண்ட அலைநீளம் அதனுடைய தனிவெப்பநிலை T க்கு எதிர் மாறு விகிதத்தில் இருக்கும் எனப் பகருகிறது. வெப்பவியக்கவியல் அடிப்படையில் இவ்விதியை 1893 ஆம் ஆண்டில் நிறுவிய வில்லெம் வீன் என்பவரின் பெயரில் இவ்விதி அழைக்கப்படுகிறது.

• இங்கு, λmax - உயர் அலைநீளம்,T - கரும்பொருளின் தனி வெப்பநிலை,b = 2.8977685(51)×10−3 m·K, விகித மாறிலி, அல்லது வீனின் இடப்பெயர்ச்சி மாறிலி என அழைக்கப்படுகிறது
• கட்புலனாகும் நிறமாலைக்குக் கிட்டவாக உள்ள அலைநீளங்களுக்கு, மீட்டர் அளவுக்குப் பதிலாக நானோமீட்டர் அளவு பயன்படுத்தப்படுகிறது. இங்கு, b = 2897768.5(51) nm·K ஆகும்.
• பிளாசுமா வெப்பநிலைகளில் இலத்திரன்வோல்ட் அலகு பயன்படுத்தப்படுகிறது. இங்கு விகித மாறிலி b = 249.71066 nm·eV ஆகும்.

ஸ்டெஃபான் போல்ட்ஸ்மென் விதி (Stefan Boltzmann law) 

• ஸ்டெஃபான் போல்ட்ஸ்மென் விதியின்படி, கருப்பொருளின் ஓரலகு பரப்பினால் ஓரலகு நேரத்தில் கதிர்வீசப்படும் வெப்ப ஆற்றலின் மொத்த அளவு, அக்கருப்பொருளின் கெல்வின் வெப்பநிலையின் நான்குமடி மதிப்புக்கு நேர்த்தகவில் இருக்கும். 
• E  = σ T 4 , 
• விகிதாச்சாரத்தின் மாறிலி ,, Stefan-Boltzmann மாறிலி என்று அழைக்கப்படுகிறது . அதற்கு ஒரு மதிப்பு உண்டு
• σ =5.670 374 419 ... × 10 ⁻⁸  W⋅m ⁻² ⋅K ⁻⁴ .
• பொதுவான வழக்கில், கதிரியக்க வெளியேற்றத்திற்கான ஸ்டீபன்-போல்ட்ஸ்மேன் சட்டம் வடிவம் பெறுகிறது

நியூட்டனின் குளிர்வு விதி

• உயர் வெப்பநிலையிலள்ள ஒரு பொருள் வெப்பத்தை இழக்கும் வீதம்,அப்பொருளுக்கும், சுற்றுப்புறச் சூழலுக்கும் இடையிலான வெப்பநிலை வேறுபாட்டிற்கு நேர்த்தகவில் இருக்கும்.

டேஞ்ஜென்ட் விதி

• ஒன்றுக்கொன்று நேர்க்குத்தான இரு காந்தப் புலங்கள் செயல்படும் புள்ளியில் தொங்கவிடப்பட்டுள்ள காந்த ஊசியானது, அவ்விரு புலங்களின் தொகுபயன் புலத்தின் திசையில் ஓய்வு நிலைக்கு வரும்.

கூலும் விதி

1. கூலும் விதி கூலும் விதி கூலுமின் டோர்சன் பலன்சு கூலும் விதி (Coulomb's law, கூலோமின் விதி), அல்லது கூலுமின் நேர்மாற்று இருபடி விதி (Coulomb's inverse-square law) என்பது, மின்னூட்டப்பட்ட மின்மங்களுக்கு இடையிலான நிலைமின் இடைவினைகளை விளக்கும் இயற்பியல் விதியாகும். 1780களில் சார்லசு அகுசிட்டின் டி கூலும் என்பவர், இத்தொடர்பை ஒரு சமன்பாடாக விளக்கினார்.
2. கூலும் விதியின்படி, இரு புள்ளி மின்னூட்டங்களுக்கு இடையேயான மின்னிலை விசையின் எண்ணளவானது, ஒவ்வொரு மின்னூட்டங்களின் எண்ணளவு பெருக்கத் தொகைக்கு நேர்த்தகவிலும், அவற்றுக்கு இடையே உள்ள தொலைவின் இருமடிக்கு எதிர்த் தகவிலும் அமையும்

${\displaystyle �={�}_{\mathrm{e}}\frac{{�}_1{�}_2}{{�}^2}}$

இதில் நேர்விசை விரட்டுவதாகவும், எதிர்விசை கவருவதாகவும் இருக்கும். இதன் விகித மாறிலிக்கு Ke கூலும் மாறிலி என்று பெயர் . இது சுற்றுப்பரப்பின் தன்மையோடு தொடர்பு உடையது. இதை கீழ் உள்ளவாறு சரியாக கணக்கிடப்படும்,

காஸ் விதி

1. இயற்பியலில், காஸ் விதி (Gauss' law) காஸ் பாய விதி என்றும் அறியப்படுகிறது. இவ்விதி, எந்தவொரு மூடிய பரப்பின் வழியே செல்லும் மின்புலப் பாயத்தையும், அப்பரப்பினுள் உள்ள மொத்த மின்னூட்டத்தையும் தொடா்புபடுத்துகிறது.
2. இவ்விதியின்படி, எந்தவொரு மூடிய பரப்பில் செயல்படும் மின்புலத்தின் மொத்த பாய மதிப்பு (ΦE ), அப்பரப்பில் உள்ள மொத்த மின்னூட்டத்தின் 1/ε0 மடங்குக்குச் சமம்.
3. 
4. இந்த மூடப்பட்ட கற்பனைப் பரப்பு காஸ்ஸியன் பரப்பு என்றழைக்கப்படுகிறது. S என்ற மூடிய பரப்பின் வழியே செல்லும் மின்புலப் பாயம் (E) பரப்பினுள் உள்ள மொத்த மின்னூட்டத்தின் மதிப்பை மட்டுமே சாா்ந்தது. ஆனால், அம்மின்னூட்டங்கள் அமைந்துள்ள இடத்தைச் சாா்ந்ததல்ல என காஸ் விதியிலிருந்து அறிகிறோம். பரப்புக்கு வெளியே உள்ள மின்னூட்டங்கள் மின்புலப் பாயத்திற்கு காரணமாவதில்லை.
5. காஸ்விதி, இயற்பியலில் உள்ள பல்வேறு பகுதிகளில் உள்ள விதிகளுடன் நெருங்கிய கணித தொடா்பினைக் கொண்டது. உதாரணமாக காந்தவியலுக்கான காஸ் விதி மற்றும் ஈா்ப்பு விசைக்கான காஸ்விதி ஆகிய விதிகளுடன் நெருங்கிய கணித தொடா்பினைக் கொண்டுள்ளது. எந்தவொரு தலைகீழ் இருமடி விதியும் காஸ் விதியை போன்று உருவாக்கப்படலாம். காஸ் விதி, கூலும் விதியின் தலைகீழ் இருமதி விதிக்கு சமமாகும். அதே போல் ஈர்ப்பு விசைக்கான காஸ் விதி, நியுட்டனின் ஈா்ப்பு விதியின் தலைகீழ் இருமடிக்கு சமமாகும்.

கிர்ச்சாஃபின் முதல் விதி (மின்னோட்ட விதி)

1. எந்த ஒரு சந்தியிலும் சந்திக்கின்ற மின்னோட்டங்களின் குறியியல் கூட்டுத்தொகை (Algebraic Sum) சுழியாகும். இது மின் துகள்களில் உள்ள மின்னூட்டங்களின் அழிவின்மை விதியின் அடிப்படையில் அமைகிறது. சந்திகளில் மின் துகள்கள் உருவாக்கப்படுவதோ அழிவதோ இல்லை. அதாவது சந்தியில் நுழையும் மின் துகள்கள் அனைத்தும் சந்தியை விட்டு வெளியேறும். கிர்க்காஃப் முதல் விதியைப் பயன்படுத்தும் போது சந்தியை நோக்கிச் செல்லும் மின்னோட்டம் நேர்க்குறி எனவும் சந்தியை விட்டு வெளியேறும் மின்னோட்டம் எதிர்க்குறி எனவும் எடுத்துக்கொள்ளப்படும்.

2. I1+I2-I3–I4 – I5 = 0 (அல்லது)

   I1+I2=I3+ I4 + I5

3. இவ்விதி மின்னூட்ட அழிவின்மை விதியின் படி செயல்படுகிறது.

கிர்ச்சாஃபின் இரண்டாம் விதி

• ஒரு மூடிய மின்சுற்றின் வெவ்வேறு பகுதிகளில் உள்ள மின்தடை (R) மற்றும் மின்னோட்டம் (I) ஆகியவற்றைப் பெருக்கிவரும் அளவுகளின் குறியியல் கூட்டுத்தொகை அம்மூடிய சுற்றில் உள்ள மின்னியக்கு விசைகளின் குறியியல் கூட்டுத் தொகைக்குச் சமம்.
• இவ்விதி ஆற்றல் அழிவின்மை விதியின் படி செயல்படுகிறது.

ஃபாரடேயின் மின்னாற்பகுதல் விதிகள்

ஃபாரடேயின் முதல் விதி

1. மின்னாற்பகுத்தலின் போது மின்முனைகளில் விடுவிக்கப்படும் பொருளின் நிறையானது (m) மின்கலத்தின் வழியே பாயும் மின்னோட்டத்தின் அளவிற்கு (Q) நேர்விகிதத்திலிருக்கும்.
2. i.e maQ 
3. மின்னோட்டத்தின் அளவானது, மின்னேற்றத்துடன் பின்வரும் சமன்பாட்டின் மூலம் தொடர்பு படுத்தப்படுகிறது என்பதை நாம் அறிவோம். I = Q/t ⇒ Q = It
4. ஃ m α It (or) m = Z It              
5. இங்கு Z என்பது மின்முனையில் விடுவிக்கப்பட்ட பொருளின் மின்வேதிச் சமானம் ஆகும்.
6. I = 1A மற்றும் t = 1 விநாடி, Q = 1C , எனில் அத்தகைய நேர்வுகளில் சமன்பாடு (9.33) ஆனது சமன்பாடு (9.34) போல மாறுகிறது 
7. ⇒  m = Z              
8. அதாவது, மின்வேதிச் சமானம் என்பது 1 கூலூம் மின்னூட்டத்தால் மின்முனையில் விடுவிக்கப்பட்ட பொருளின் அளவு என வரையறுக்கப்படுகிறது.

ஃபாரடேயின் இரண்டாம் விதி

1. ஒரே அளவு மின்னோட்டத்தை வெவ்வேறு மின்பகுளிக் கரைசல்களின் வழியே செலுத்தும்போது, மின்முனைகளில் விடுவிக்கப்படும் பொருளின் அளவானது அவற்றின் மின்வேதிச் சமானங்களுக்கு நேர்விகிதத்திலிருக்கும்.
2. m α E

மின்காந்தத் தூண்டல் பற்றிய ஃபாரடே விதிகள்

முதல் விதி

• ஒரு மூடப்பட்ட கற்றோடு தொடர்பு கொண்ட காந்தப் பாயம் மாறும் பொழுது அந்த கற்றில் மின்னியக்கு விசை தூண்டப்படுகிறது. காந்தப் பாயத்தின் மாற்றம் நிகழ்ந்து கொண்டிருக்கும் வரையில் மட்டுமே தூண்டப்பட்ட மின்னியக்கு விசை நீடிக்கும்.

இரண்டாம் விதி

• மூடப்பட்ட கற்றில் தூண்டப்பட்ட மின்னியக்கு விசையின் எண்மதிப்பு, சுற்றுடன் தொடர்பு கொண்ட காந்தப் பாயம் மாறும் வீதத்திற்கு நேர்த்தகவில் இருக்கும்.

மேக்ஸ்வெல்லின் வலக்கை திருகு விதி

• மின்னோட்டம் பாயும் கடத்தியைச் சுற்றி அமைந்துள்ள காந்தவிசைக் கோடுகளின் திசையானது, வலது கை திருகு ஒன்றினை மின்னோட்டம் செல்லும் திசையில் செலுத்தும் போது, திருகு சுழலும் திசையால் பெறப்படும்.

பயட் - சாவர்ட் விதி (BIOT - SAVART LAW)

1. ஆர்ஸ்டெட்டின்கண்டுபிடிப்பைத் தொடர்ந்து, ஜீன் - பாப்டிஸ்ட் பயட் மற்றும் பெலிக்ஸ் சாவர்ட் இருவரும் 1819 இல் மின்னோட்டம் பாயும் கடத்திக்கு அருகே வைக்கப்பட்ட காந்தம் உணரும் விசையை அளந்தறியும் சோதனைகளை மேற்கொண்டு கணிதவியல் சமன்பாட்டை உருவாக்கினார்கள்.
2. இச்சமன்பாடு வெளியில் ஒரு புள்ளியில் உருவாகும் காந்தப்புலத்தை, அக்காந்தப்புலத்தை உருவாக்கும் மின்னோட்டத்தின் அடிப்படையில் கணக்கிடுகிறது. இது எல்லா வித வடிவ அமைப்புள்ள கடத்திகளுக்கும் பொருந்தும்.

காந்தத் தூண்டல்

• மின்னோட்டத்திற்கு (1) நேர்த்தகவிலும்
• மின்னோட்டக் கூறின் நீளத்திற்கு நேர்விகிதத்திலும் (dl)
• கோண சைன் மதிப்பிற்கு sin 0 நேர்த்தகவிலும்
• தொலைவின் இருமடிக்கு (r2) எதிர்த்தகவிலும் இருக்கும்.

• இதனை பின்வருமாறு எழுதலாம்

  
  

  
  

  இங்கு k = μo/ 4π(SI அலகில்)

  வெக்டர் குறியீட்டின்படி,

 

ஆம்பியரின் சுற்று விதி

• ஆம்பியரின் விதி : ஒரு மூடிய வளையத்தின் மீதுள்ள காந்தப்புலத்தின் கோட்டு வழித் தொகையீட்டு மதிப்பு (Value of line integral) சுற்று அவ்வளையத்தினால் மூடப்பட்ட நிகர மின்னோட்டத்தின் μ0 மடங்கிற்குச் சமம்.

• திருத்தப்பட்ட ஆம்பியர் விதி (தொகையீட்டு வடிவில்):

  ${\displaystyle {\oint }_{�}\mathbf{�}\cdot �\mathbf{�}={\iint }_{�}\mathbf{�}\cdot �\mathbf{�}+\frac{�}{��}{\iint }_{�}\mathbf{�}\cdot �\mathbf{�}}$

  இதில்

  ${\displaystyle \mathbf{�}=�\mathbf{�}}$ - பெயர்ச்சி மின்னோட்ட அடர்த்தி (ஆம்பியர் / சதுர மீட்டரில்).

  வகையீட்டு வடிவில் "ஆம்பியர் - மேக்ஸ்வெல் விதி" பின்வருமாறு அமையும்:

  ${\displaystyle \mathrm{\nabla }\times \mathbf{�}=\mathbf{�}+\frac{\mathrm{\partial }\mathbf{�}}{\mathrm{\partial }�}}$

  இதில் இரண்டாவது பகுதி பெயர்ச்சி மின்னோட்டத்தால் விளைவது.

முனை விதி

• ஒரு முனையிலிருந்து நோக்கும் போது வரிச்சுருள் வழியே பாயும் மின்னோட்டம் வலஞ்சுழியாக அமைந்தால் அருகே உள்ள முனை தென்முனை ,சேய்மையில் உள்ள முனை வடமுனை.

லென்ஸ் விதி

1. ஒரு சுற்றில் தூண்டப்பட்ட மின்னோட்டத்தின் திசை, எப்போதும் அதை உருவாக்கக் காரணமாக இருந்த, காந்தப் பாய மாற்றத்தை எதிர்க்கும் வகையில் அமையும்.
2. லென்சின் விதி, ஹைன்ரிக் எமில் லென்சு என்ற ஜெர்மானிய இனத்தைச்சேர்ந்த உருசிய இயற்பியலாரால் உருவாக்கப்பட்டது.
3. இவ்விதி இவரின் பெயரினால் 1834 ஆம் ஆண்டு முதல் குறிப்பிடப்படுகிறது

லென்சு விதியின் கூற்று பின்வருமாறு:

ஒரு மின்சுற்றில் மின்னியக்க விசை தூண்டப்படும் போது, தூண்டப்பட்ட மின்னோட்டம் அதை உண்டாக்கக் காரணமாயிருந்த காந்தப்பாய்வின் மாற்றத்தை எதிர்க்கும் முறையில் அமையும். (அல்லது)

(காந்தப்புல மாற்றத்தினால் ஒரு கம்பிச்சுருளில் உருவாகும்) தூண்டு மின்னோட்டத்தினால் ஏற்படும் காந்தப்புலம், அது உருவாவதற்குக் காரணமாயிருந்த (காந்தப்புல) மாற்றத்தை எதிர்க்கும் விதத்தில் அமையும். (அல்லது)

ஒரு கம்பிச்சுருளில் உருவாகும் தூண்டு மின்னோட்டம், அதை உருவாக்கிய மாற்றம் அல்லது காரணத்தை எதிர்க்கும் வகையில் பாயும்.

புருஸ்டர் விதி

• தளவிளைவுக் கோணத்திற்கும், ஒளி விலகல் எண்ணிற்கும் இடையேயான தொடர்பு பற்றி விளக்குகிறது.
• தள விளைவுக் கோணத்தில் ஒளிக்கற்றை படும் போது எதிரொளிக்கும் கதிரும், விலகலடைந்த கதிரும் ஒன்றுக்கொன்று செங்குத்தாக அமையும்.
• தளவிளைவுக் கோணத்தின் டேஞ்சன்ட் மதிப்பு எண்ணளவில் அந்த ஊடகத்தின் ஒளிவிலகல் எண்ணிற்குச் சமம்.

மோஸ்லே விதி

1. மோஸ்லியின் விதி (Moseley's law) என்பது அணுக்களில் இருந்து வெளிவிடப்படும் எக்சு-கதிர்களின் பண்புகளைக் குறித்த ஒரு அனுபவ விதியாகும். இவ்விதி 1913ஆம் ஆண்டில் ஹென்றி மோஸ்லி என்னும் ஆங்கில இயற்பியலாளரால் தெரிந்து விளக்கப்பட்டது. 
2. எக்சு-கதிர்கள், வெற்றிடக் குழாயிலுள்ள இலக்கினை, வேகமாகச் செல்லும் இலத்திரன்கள் மோதுவதால் தோற்றுவிக்கப்படுகின்றன. இந்நிலையில் தொடர்நிறமாலையுடன் இலக்காகப் பயன்படும் தனிமத்தின் பண்புக் கோடுகளும் (Characteristic lines) தோற்றுவிக்கப்படுகின்றன. மோஸ்லி பல்வேறு தனிமங்களை இலக்காகப் பயன்படுத்தி, அவை ஒவ்வொன்றின் பண்புக் கோடுகளையும் ஆய்ந்தார். பிராக்கின் எக்சு கதிர் நிறமாலைமானியினைப் (Bragg's x-ray spectrometer) பயன்படுத்தி அவர் மேற்கொண்ட ஆய்வுகள் மிகவும் விந்தையான முடிவுகளைக் காட்டின. முக்கியமாக பண்பு நிறமாலையில் KLM கோடுகள் உள்ளதைக் கண்டார்.
3. K பண்புக் கோடுகளின் அதிர்வெண்கள், அணு எண் கூடும் போது அதிகரிக்கிறது. இதற்கு முக்கிய காரணம் அணுஎண் கூடும் போது K எலக்ட்ரான்களின் பிணைப்பாற்றலும் கூடுவதாகும்.
4. Kα வரியினை எடுத்துக்கொள்வோம். அதிக அணுவெண்ணுள்ளத் தனிமத்திற்கு Kα கதிரின் அதிர்வெண்ணும் அதிகமாக இருக்கும்.
5. அதாவது:

• இதில் f, கதிரின் அதிர்வெண்; Z என்பது அணு எண்; a யும் b யும் மாறிலிகள். a, b என்பன K தொடருக்கு மாறுவதில்லை. ஆனால் L தொடருக்கு மாறும். b என்பது கரு மறைப்பு மாறிலி (Neuclear screening constant) எனப்படும். இதன் மதிப்பு L தொடருக்கு அதிகம். இதுவே மோஸ்லி விதியாகும்.

 

ஒளியின் உமிழ்தலின் விதிகள்

விதி : 1

• குறிப்பிட்ட ஒளி உணர்திறன் மிக்க பொருளிற்கு, ஒளியின் செறிவு எவ்வளவு அதிகம் இருப்பினும், எந்த அதிர்வெண்ணிற்கும் கீழ் ஒளியின் உமிழ்தல் முற்றிலும் நிகழாதோ, அந்த படுகதிரின் சிறும அதிர்வெண் பயன் தொடக்க அதிர்வெண் எனப்படும்.

விதி : 2

• குறிப்பிட்ட ஒளி உணர்திறன் மிக்க பொருளிற்கு, படுகதிர்வீச்சின் அதிர்வெண் ஆனது பயன் தொடக்க அதிர்வெண்ணை விட அதிகமாக இருக்கும்போது, ஒளி மின்னோட்டமானது படுகதிரின் செறிவிற்கு நேர்த்தகவில் இருக்கும்.

விதி : 3

• ஒளிமின் உமிழ்வு ஒரு உடனடி நிகழ்வாகும். அதாவது கதிர்வீச்சு படுவதற்கும், ஒளி எலக்ட்ரான்கள் உமிழப்படுவதற்கும் இடையில் காலப் பின்னடைவு இருக்காது.

விதி : 4

• ஒளி எலக்ட்ரான்களின் பெரும் இயக்க ஆற்றல் படுகதிரின் அதிர்வெண்ணிற்கு நேர்த்தகவில் இருக்கும்: செறிவினைச் சார்ந்தது அல்ல.

கதிரியக்கச் சிதைவு விதி

• ஓரலகு நேரத்தில் சிதைவடையும் அணுக்களின் எண்ணிக்கை (சிதைவு வீதம்) அந்நேரத்தில் அத்தனிமத்தில் உள்ள அணுக்களின் எண்ணிக்கைக்கு நேர்தகவில் அமையும்.